D’après l’INSEE, jusqu’en 1976, les achats de tabac augmentaient de 3,5% par an. A la suite d’une première augmentation importante du prix du tabac, cette hausse de consommation est passée à 2,4% par an jusqu’en 1991. Puis après la loi Evin le prix du tabac a été multiplié par 3  entre 1991 et 2005. Les achats ont alors baissé en volume de 3,5% par an, mais augmenté en valeur de 5,7% par an en moyenne.
    La loi a interdit la vente du tabac aux mineurs de moins de 16 ans, mais cette mesure est largement contournée par les jeunes. Puis à partir de 2007 fumer dans un lieu public fermé est interdit. Le prix de la cigarette a continué d’augmenter, la vente de cigarette a nettement baissé, mais les achats dans les pays frontaliers et en contrebande se sont énormément développés.
    Le nombre de fumeurs a beaucoup baissé entre 2016 et 2019, puis est resté stable.
    La France se situerait dans la moyenne européenne (27% de fumeurs quotidiens chez les hommes et  21% chez les femmes en 2022), mais parmi les pays les plus consommateurs d’Europe de l’Ouest. Cela représente environ 12 millions de personnes.
     Le tabagisme a diminué chez les adolescents de 17 ans (25,1% de fumeurs quotidiens à 15,6%
     Le nombre de fumeurs quotidiens reste en 2022 nettement plus élevée lorsque le niveau de diplôme est plus faible : elle varie de 30,8 % parmi les personnes n’ayant aucun diplôme ou un diplôme inférieur au baccalauréat à 16,8 % parmi les titulaires d’un diplôme supérieur au baccalauréat. Le pourcentage est la plus élevé parmi le tiers de la population dont les revenus sont les plus bas (33,6 %); enfin, le nombre de fumeurs quotidiens reste nettement plus élevée parmi les personnes au chômage (42,3 %), que parmi les actifs occupés (26,1 %) ou les étudiants (19,1 %).
     Les statistiques de 2021 montrent que, parmi les fumeurs quotidiens, 59,3% déclarent avoir envie d’arrêter de fumer, 26,4% déclarent avoir le projet d’arrêter dans les 6 prochains mois et 30,3% ont fait une tentative d’arrêt d’au moins une semaine dans les 12 derniers mois. Les hommes fumeurs sont plus nombreux que les femmes fumeuses à avoir envie d’arrêter de fumer (61,7% vs 56,5% des femmes). Mais ce sont des déclarations !

    La cigarette électronique a fait baisser la consommation, mais elle a aussi séduit de nouveaux fumeurs. Environ 6% des Français ont essayé la cigarette électronique, et 1% l’utilisent. Cela représente tout de même 500 000 personnes. Par rapport à la cigarette, c’est une moins mauvaise chose pour les fumeurs et c'est une façon d’arrêter. Mais cela reste un produit nocif : il ne faut pas que cela remette la fumée à la mode.
    Bref on ne sait pas comment enrayer cette addiction qui coûte cher à la communauté, mais bien plus au fumeurs, tant financièrement qu’au plan de leur santé.
    La Cour des comptes a écrit que si le tabac rapporte 45 milliards d’euros par an à la France, il lui coûte 75 milliards en dépenses de santé. Et la puissance des lobbies du tabac est énorme et elle nous demande de nous apitoyer sur le sort des buralistes, dont pourtant le revenu a plutôt augmenté.

    Les chiffres de mortalité des fumeurs sont énormes et pourtant de récentes études ont montré qu’ils étaient sous-estimés, probablement d’environ 20%.
    On estime qu’avec les progrès de la médecine dans la lutte contre les maladies, bientôt une personne sur deux mourra du fait du tabac dans les prochaines décennies 
    Un exemple illustre bien ce risque. Avec des camarades de la même promotion d’ingénieurs, nous faisions le point sur les camarades encore en vie, et nous nous sommes aperçu que parmi ceux qui fumaient environ 1/2 paquet de cigarettes par jour, ou plus, seuls deux étaient encore en vie, parmi nous qui avions entre 82 et 85 ans. Aujourd'hui où j'ai 91 ans, il n'y en a plus aucun de vivant.
    Les fumeurs meurent, en moyenne, dix ans plus tôt que les non-fumeurs
    Si le cancer du poumon est la maladie la plus connue et celle dont le lien avec le tabac est le plus indiscutable, (90 % des malades sont fumeurs ou l'ont été), il en existe de nombreuses autres dont la responsabilité est établie depuis longtemps : les cancers de l'œsophage, de la vessie, du pancréas, la broncho-pneumopathie chronique obstructive, le diabète, les accidents vasculaires cérébraux…
    Mais une étude anglaise récente a identifié une quinzaine de nouvelles causes de décès prématurés liées au tabac, la probabilité de mourir d’un cancer du sein étant augmentée de 30% et de la prostate de 45%. Les risques de mort d’insuffisance rénale sont multipliés par deux, et l’AVC n’est pas le seul risque puisque le risque d’obturation des artères du système intestinal est multiplié par six.
    L’étude anglaise indique que l’estimation du nombre de décès annuels dus au tabac aux USA, devrait ainsi passer de 440 à 500 000. En France elle devrait passer de 78 000 à 90 000 environ.
    
    Ce qui me paraît grave également c’est le risque pour les jeunes qui souvent commencent à fumer vers 15/16 ans et qui n’ont pas encore un cerveau entièrement formé.
    Des études récentes montrent qu’à cet âge, le système nerveux est beaucoup plus sensible à la nicotine, et à d’autres produits liés à la fumée du tabac, et il suffit de quelques cigarettes pour que l’addiction s’installe.
    Et la nicotine s’attaque aux mécanismes de l’attention et à l’hippocampe, « notre professeur de la mémoire » et les résultats scolaires peuvent s’en ressentir profondément.
    Le plus absurde, c’est que au plan physiologique, le tabac n’apporte au début aucun plaisir : il vous empêche au contraire de ressentir le goût de la nourriture. Le plaisir ne vient ensuite que lié au manque de nicotine que la consommation de tabac soulage.
    En fait on ne fume les premières fois que bêtement, pour faire comme les copains, pour ne pas avoir l’air de reculer, au sein du groupe. C’est l’effet moutonnier du « t’es pas cap », qui a toujours existé, mais qui s’est beaucoup développé avec la multiplication des psychologies de groupe liée au développement du numérique.
    Et les jeunes s’aperçoivent un jour qu’ils sont pris au piège et que cela leur coûtera un jour la vie.

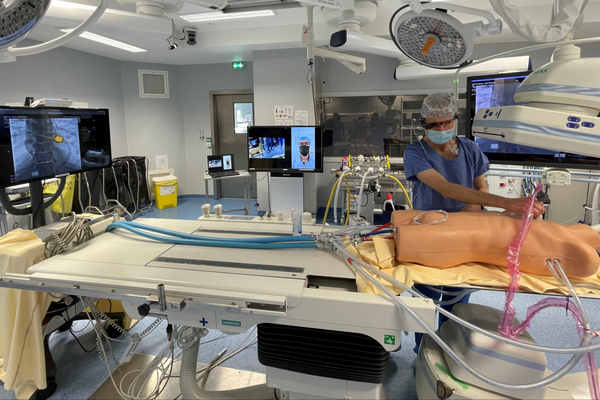
      Chirurgien est un métier bien difficile.
    D’une part il faut avoir les connaissances habituelles à tout médecin, mais encore il faut de super connaissances en anatomie.
    Je me souviens d’un chirurgien avec lequel je discutais et qui me décrivait une opération, en me donnant tous les détails de ce qu’il allait rencontrer successivement en faisant ses incisions : muqueuses, muscles, nerfs, vaisseaux sanguins, organes, pout arriver sur ce qu’il devait opérer. C’était une véritable carte en 3D.
    Et puis non seulement il faut des connaissances et une expérience intellectuelles, mais il faut une grande dextérité pour manier les instruments avec précision surtout pour inciser, mais aussi pour recoudre. Et il faut calme et concentration et que la main ne tremble pas.
    J’ai beaucoup d’admiration pour cette capacité d’action.

    L’apprentissage d’un chirurgien est donc très long. Non seulement 10 ans d’études de médecine et de spécialité, mais l’acquisition d’expérience au sein d’une équipe, auprès des chirurgiens plus anciens.
    Il est bien connu qu’en fac de médecine, avant d’oser intervenir sur une personne, les étudiants apprenaient à manier le scalpel et à étudier l’anatomie sur des cadavres. Ce n’est pas nouveau et de nombreuses peintures de maîtres en témoignent.
    Mais un cadavre n’est pas un être vivant et ce n’est pas une véritable opération.
    Les facs de médecine avaient donc des blocs opératoires avec une salle d’observation où les étudiants pouvaient suivre des opérations réelles ou bien des caméras qui filmaient l’opération et retransmettait l’image dans un amphi. Des anesthésistes et des infirmier(es) pouvaient aussi apprendre ainsi leur métier.

    Ces pratiques se modernisent.
    Déjà étaient apparus des mannequins interactifs sur lesquels certaines interventions pouvaient être faites
    Les cadavres évoluent. Ce sont toujours des personnes décédées mais dont le corps a été mis au congélateur et réchauffé quelques heures juste avant la séance opératoire, pour repasser de -22 à + 37 d°C.
    Mais une petite installation hydro-pneumatique permet maintenant d’insuffler d’une part de l’air dans les poumons de sorte que le cadavre respire en quelque sorte, mais aussi d’injecter un liquide ayant la consistance et la couleur du sang dans ses artères, ce qui redonne même à la peau sa couleur naturelle et ses caractéristiques mécaniques presque analogues à uen personne vivante. On peut même simuler une anesthésie.
    Bref les étudiants peuvent pratiquer une véritable opération, sans risque toutefois de faire des dégâts par maladresse. Le cadavre ne criera jamais qu’on lui fait mal !!!
    Et la machinerie peut être programmée pour entraîner des incidents non pévus par les chirurgiens, pour les habituer à avoir les bonnes réactions.

    Autre progrès, on continue à filmer des opération, mais avec des caméras 3D et le film peut être envoyé sur des lunettes 3D de « réalité virtuelle ».
    C’est la même technique que dans les jeux vidéo ou dans certains musées ou visites de lieux aux architectures de l’antiquité où l’on reconstitue ce qu’étaient autrefois les monuments.
    L’étudiant voit ce que voit le chirurgien, comme s’il avait la tête au dessus du champ opératoire et il peut assister à l’opération comme s’il était à sa place, si ce n’est que ce n’est pas lui qui manie les instruments, alors que dans un jeu, c’est vous qui commandez les gestes (ou de même dans un simulateur de vol pour pilotes).

    Mais au delà de la formation technique des spécialistes, il sera d’une part possible de donner une certaine information au malade (s’il le souhaite et avec prudence, car cela peut être traumatisant avant une opération qu’on va subir soi même), au besoin après l’intervention. D’autre part des applications simplifiées analogues aux jeux sont disponibles sur smartphone en le reliant à un « masque 3D ». On peut jouer à l’apprenti chirurgien et cela pourra peut être susciter  des vocations.

    Ces divers moyens ont effectivement un but d’apprentissage technique et manuel, mais aussi psychologique, car l’étudiant doit s’habituer au stress des premières opérations, car le risque est toujours présent. L’apprentissage des internes auprès des anciens restera donc toujours nécessaire, mais ils auront été mieux formés au préalable.

La photo en début d'article présente une simulation d'opération chirurgicale dans une des salles d'cpérations du CHU de Rennes.
Les deux photos en fin d'article montrent des lunettes de réalité virtuelle pour suivre une opération et une simulation sur smartphone, genre jeu vidéo. (Google Play)

   Je suis toujours étonné quand j’entends des gens, que je pensais intelligents dire : « il faut se passer de l’énergie nucléaire » ou « il faut se passer de l’expérimentation animale ». Je pense qu’ils n’ont pas beaucoup réfléchi à la question.

    Que l’on ne doive pas considérer les animaux comme des objets et qu’on ne les fasse pas souffrir, je suis entièrement d’accord. En particulier qu’on n’achète pas un animal de compagnie pour l’abandonner ensuite, qu’on évite de faire souffrir les animaux qui nous servent ensuite de nourriture.
    Pourtant cela ne nous viendrait pas à l’esprit de dire la même chose des plantes et pourtant ce sont aussi des êtres vivants!
    Mais je pense qu’il faut encore être plus vigilant vis à vis de la vie et de la souffrance des humains. Et quant je vois une artiste américaine veniur reprocher à la France de gaver des oies, je voudrais lui dire de s’occuper du centre de Guantanamo ou des agissements de la CIA.
    Cependant je voudrais revenir sur le problème des expérimentations animales. Certes il faut éviter de faire souffrir les animaux et veiller aux conditions de ces essais, mais peut on s’en passer?

    Je parlerai d’abord des médicaments : avant de les mettre dans le commerce, il faut s’assurer qu’ils sont efficaces, qu’ils ne sont pas dangereux, et ceci à diverses doses, et aussi connaître les effets secondaires indésirables.
    L’expérimentation finale est faite sur des humains, en hôpital.
    Mais elle n’est pas sans danger et on a vu récemment qu’une telle expérimentation a causé la mort d’un homme et des séquelles graves chez plusieurs autres. Et il y avait eu pourtant une sévère et longue expérimentation animale. Sans elle il y aurait eu certainement plusieurs morts et handicapés graves si on s’en était tenu à la seule expérimentation humaine, sans autre préalable.
    S’il n’y avait pas eu d’expérimentation animale, nous n’aurions aucun vaccin, pas d’antibiotique et pas la plupart des médicaments très actifs. Il y aurait tous les ans des dizaines de millions de morts supplémentaires de maladies.
    Au départ on ne sait pas grand chose du fonctionnement du corps humain, ni de celui des bactéries et virus. Sans l’expérimentation sur ls animaux de la mouche drosophile à la souris, puis , moins souvent sur d’autres mammifères, nous ne saurions pas grand chose sur les mécanismes de physiologie et des maladies qui nous affectent.
    L’expérimentation animale est indispensable aux études scientifiques, car l’étude de thérapeu- tiques et de médicaments ne peut se faire que si on connaît suffisamment au préalable les maladies et le fonctionnement du corps humain.
    On a trouvé des traces du virus Zika dans le liquide amniotique et le cerveau d'un fœtus anormal; une culture sur des neurones a montré in vitro des perturbations apportées par le virus . Mais pour être absolument certain de son action, des essais sont nécessaire in vivo sur des souris en gestation pour démontrer l'action tératogène.

    Et l’expérimentation animale n’a jamais autant été encadrée qu’aujourd’hui.
    Deux directives sur la protection des animaux existent de 1986 et de 2010.
    Les animaux sont utilisés au minimum (tellement même que probablement si on les avait davantage utilisés, il n’y aurait pas eu un mort dans les derniers essais thérapeutiques).
Des seuils sont respectés pour limiter une éventuelle souffrance et les animaux sont insensibilisés ou traités par analgésiques. Les conditions d’élevage sont strictement réglementés de même que les conditions de soins et de chirurgie.
    Des comités d’éthiques ont été créés, ainsi que des contrôles des animaleries et laboratoires. Pour utiliser certaines espèces il faut démontrer qu’un ne peut pas utiliser des animaux moins évolués (notamment pour le singe).

    Ce qui m’agace, dans ce domaine, c’est que les gens qui critiquent l’expérimentation animale et demandent son abolition, n’ont aucune notion de biologie, de ce à quoi servent ces expérimen- tations et sont les premier à hurler quand les médicaments destinés à l’homme ne sont pas d’une efficacité parfaite.
    Il est évidemment beaucoup plus facile de critiquer ce que l’on ne connaît pas, parce qu’on ne se rend pas compte alors qu’on ne dit que des âneries.

   

      
           On me demande  à nouveau quel est l’influence de l’environnement sur notre patrimoine génétique et qu’est ce que l’épigénétique.
           Je vous ai parlé plusieurs fois de « l’épigénétique ». ( mes articles des 29 et 30/10/2020)
          Plutôt que de vous renvoyer sur mes anciens articles, je vais essayer de les résumer.

           Le terme d’épigénétique inventé en 1942 par Conrad Waddington concernait à l’origine  « la branche de la biologie qui étudie les relations de cause à effet entre les gènes et leurs conséquences biologiquess, et concernait donc le phénotype » (notre structure héréditaire ADN.)
          Aujourd'hui, la définition la plus courante de l’épigénétique est « l’étude des changements héréditaires dans la fonction des gènes, ayant lieu sans altération de la séquence d’ADN ».
         Je rappelle que l’ADN est une structure moléculaire en double hélice de deux mètres de long, dans le noyau d’une cellule qui ne fait que quelques micromètres. L’échelle élémentaire de l’ADN c’est le nanomètre. (10^-9 m)
         L'ADN est une espèce d’échelle avec deux montants hélicoïdaux (composés de phosphates et de sucres) et de barreaux, constitués chacun de deux molécules parmi quatre bases azotées que nous nous contenterons d’appeler (un peu comme Bach avec les notes) A, C, G, T et qui s’associent toujours A et T, (ou T et A) et C et G (ou G et C).
        C’est l’enchaînement des séquences successives de ces molécules (les barreaux) qui constituent le patrimoine génétique d’une cellule, c’est à dire l’enchaînement des nucléotides A,C,G,T.
        Tout le fonctionnement biologique de nos cellules est conditionné par de multiples protéines, qui sont issues de 20 molécules élémentaires d’acides aminés et la synthèse d’un acide aminé donné dépend de la succession de 3 de ces bases A,C,G,T. (on appelle cette succession de 3 bases des « codons »)

       Mais “l’usine” de synthèse des acides aminés est souvent au repos et puis tout à coup, pour des raisons encore mal connues, une portion de cette succession de base va s’activer et fabriquer la succession d’acides aminés et donc la protéine spécifique que code cette succession.
       C’est cette succession de “codons” de 3 bases qui code donc chaque type de protéine bien spécifique, que l’on va appeler un gêne et on dit lorsque cette fabrication entre en jeu, que le “gêne s’exprime”.

         Dans la formation du corps humain, à certains moments, certains gènes seront “forcés” de s’exprimer", sinon nous aurions une non-formation ou mal-formation.
        Mais d’autres pourront rester « endormis » toute notre vie, ou au contraire, tout à coup s’exprimer alors que ce n’était ni obligatoire ni même prévu. Cela pourra être sous l’effet de facteurs biologiques, mais aussi de phénomènes extérieurs physiques ou psychiques.
        Donc un  événement extérieur peut être capable de déclencher l’expression d’un gène. C’est cela l’épigénétique
   
       Cela dit, ce n’est pas tout à fait aussi simple que cela, car une caractéristique de notre corps, un caractère génétique, la prédisposition à une maladie ou son apparition; ne dépendent pas d’un seul gènes, mais de plusieurs qui modulent les événements épigénétiques.
      L’apparition d’une modification génétique n’est donc pas du « tout ou rien » car elle est modulée par plusieurs gènes, et tous ne s’expriment pas forcément.
       
      L’épigénétique est donc un potentiel de modifications génétiques sous l’effet d’événements internes ou externes «(nourriture, stress, traumatismes divers…), modifications qui sont ultérieures à la conception et à la naissance.
      On pourrait donc penser qu’elles n’ont aucun rapport avec notre patrimoine génétique légué par nos parents.
      Ce n’est pas tout à fait vrai.
      En effet pour s’exprimer un gène doit permettre que les éléments d’ADN le concernant, (la séquence des bases),puissent être « reproduits ».
      Pour que cette duplication se fasse il faut que l’ADN dont la chaine est enroulée sur des espèces de bobines, les histones, se déroule à l’endroit où doit se faire la transcription.
      D’autres gènes voisins peuvent bloquer ce mécanisme.
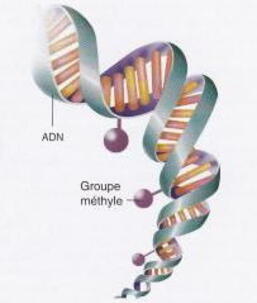
      Par exemple, la présence de groupes méthyle (-CH3) à I'ADN limite I'accès et empêche la machinerie de transcription de se lier à I'ADN, et le gène est ainsi rendu silencieux, ou du moins la probabilité de son expression est fortement diminuée.
A l'inverse, le groupes acétyle (- COCH3) fixés aux histones, conduisent au relâchement et au déroulement de I'ADN et facilitent l'expression génique, et donc sa probabilité, mais ce ne sont pas les seuls groupes chimiques concernés par ce mécanisme (voir les deux schémas en tête de l'article).
      Dans l’ADN transmis par nos parents un certain nombre de groupes favorisant ou interdisant le déroulement et donc la transcription, sont présents.
      Certaines possibilités ou impossibilités de modification épigénétiques sont donc transmises par nos parents, mais s’il est presque impossible aux gènes silencieux de s’exprimer, il n’est pas certain que ceux qui pourraient s’exprimer le fassent par la suite.
      Il faut qu’un événement les pousse à s’exprimer.

      Je trouvais commode que l’on puisse trouver chez le pharmacien, sans ordonnance, des médicaments courants et non remboursés par la sécurité sociale.
    Je m’aperçois maintenant que c’est dangereux, car malheureusement beaucoup de personnes s’en servent n’importe comment et ne lisent jamais les notices.

    On a eu l’exemple du paracétamol, qui est utile contre la douleur, voire la fièvre, mais qui ne devrait être utilisé que si on en a vraiment besoin, donc pour un temps limité et sans dépasser 3 g par jour.
    Or beaucoup de personnes en prennent dès qu’elles croient qu’elles vont avoir mal, c’est à dire presque tout le temps, alors que d’autres, qui ont entendu dire qu’on pouvait aller jusqu’à 6 cachets par jour, avalent 6 fois un comprimé d’un gramme, c’est à dire le double de la dose maximale.
    L’agence Nationale de Sécurité des médicaments (ANSM) a mis en garde  en signalant qu’on avait constaté des cas d’accidents cardiaques, dus à l’usage abusif du paracétamol. Les surdosage sont dangereux pour le foie, au point de nécessiter une greffe, par hépatite grave. On considère que c’est actuellement la première cause de greffe de foie en France.

    Un autre exemple nous est donné par des bêtises de jeunes.
    Sans doute avez vous déjà utilisé un sirop pour la toux, (ou des comprimés), contenant de la codéine, qui est un analgésique assez fort, efficace mais dangereux : c’est de la méthyl-morphine.
    Il est dangereux si on en prend trop et surtout si on en prend trop souvent, il y a un risque important d’addiction. L’utilisation de codéine peut provoquer des réactions analogues à des allergies (démangeaisons, rougeurs, nausées…), et les médecins prescrivent souvent de la prométhazine, qui est un antihistaminique modéré.
    On trouve en vente libre chez le pharmacien des sirops à la codéine et d’autres contenant de la prométhazine.
    Des jeunes ont vu sur internet que des américain faisaient, avec ces sirops un cocktail, appelé le   « purple drank » car il est violet, en les mélangeant avec des sodas voire de l’alcool, lequel cocktail a des effets relaxant et désinhibant.
    Et finalement c’est une véritable drogue, dangereuse en cas d’excès mais surtout capable d’induire une addiction tenace, et cela à partir de produits en vente libre chez le pharmacien.

    D’ailleurs les adultes mélangent aussi paracétamol et codéine pour renforcer l’effet analgésique de chacun des produits et là encore c’est dangereux et susceptible de provoquer des addictions.

    J’ai eu l’occasion de lire une notice sur un léger somnifère qui avait été conseillé à une personne de ma famille, lequel est en vente tout à fait libre et non remboursé.
J’ai été étonné de voir sur la notice qu’il était conseillé de ne pas l’employer plus de 5 jours. On ne précisait pas pourquoi. Mais alors pourquoi le mettre en vente libre. Cela m’étonnerait que toutes les personnes lisent la notice.

    Je ne suis pas contre ces médicaments, ils sont utiles, mais ce sont des produits dangereux et s’ils sont en vente libre sans ordonnance, on n’a pas de prescriptions quant aux précautions à respecter.
    Je pense que les pharmaciens devraient disposer, lorsqu’ils vendent de tels médicament d’une simili-ordonnace préimprimée et très simple, qui indique les doses et les durées à ne pas dépasser, et qu’il commentent éventuellement pour l’expliquer aux personnes qui auraient du mal à comprendre ce document.
    Il fauudrait aussi que les parents enferment les médicaments dans des armoires situées à une certaine hauteur et fermée à clé, les enfants devant demander à leur parent de leur donner les médicaments. Il est anormal qu’un enfant de 12 ans puisse aller prendre lui même, sirops à la codéine et à la prométhazine pour s’ en faire une « potion magique » qui est en réalité une drogue.